Lectures on Nonlinear Optics - Lecture 5

Quantum mechanics II: Formulation of nonlinear optical interactions

lect5.pdf [283 kB] Lecture 5 in Portable Document Format.

In the previous lecture, the quantum mechanical origin of the linear and nonlinear susceptibilities was discussed. In particular, a perturbation analysis of the density operator was performed, and the resulting system of equations was solved recursively for the n:th order density operator 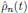$\hat{\rho}_n(t)$ in terms of 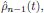$\hat{\rho}_{n-1}(t)$ , where the zeroth order term (independent of the applied electric field of the light) is given by the Boltzmann distribution at thermal equilibrium.

So far we have obtained the linear optical properties of the medium, in terms of the first order susceptibility tensor (of rank-two), and we will now proceed with the next order of interaction, giving the second order electric susceptibility tensor (of rank three).

1. The second order polarization density

For the second order interaction, the corresponding term in the perturbation series of the density operator in the interaction picture becomes [1]

$\eqalign{ \hat{\rho}'_2(t)&={{1}\over{i\hbar}}\int^t_{-\infty} [\hat{H}'_{\rm I}(\tau_1),\hat{\rho}'_{1}(\tau_1)]\,d\tau_1\cr &={{1}\over{i\hbar}}\int^t_{-\infty} [\hat{H}'_{\rm I}(\tau_1),{{1}\over{i\hbar}}\int^{\tau_1}_{-\infty} [\hat{H}'_{\rm I}(\tau_2),\hat{\rho}_0]\,d\tau_2\,]\,d\tau_1\cr &={{1}\over{(i\hbar)^2}}\int^t_{-\infty}\int^{\tau_1}_{-\infty} [\hat{H}'_{\rm I}(\tau_1), [\hat{H}'_{\rm I}(\tau_2),\hat{\rho}_0]]\,d\tau_2\,d\tau_1\cr }\eqno{(1)}$ (1)

In order to simplify the expression for the second order susceptibility, we will in the following analysis make use of a generalization of the cyclic perturbation of the terms in the commutator inside the trace, as

$\Tr\{[\hat{Q}_{\alpha}(\tau_1),[\hat{Q}_{\beta}(\tau_2),\hat{\rho}_0]] \hat{Q}_{\mu}\} =\Tr\{\hat{\rho}_0[[\hat{Q}_{\mu},\hat{Q}_{\alpha}(\tau_1)], \hat{Q}_{\beta}(\tau_2)]\}.\eqno{(2)}$ (2)

By inserting the expression for the second order term of the perturbation series for the density operator into the quantum mechanical trace of the second order electric polarization density of the medium, one obtains

$\eqalign{ P^{(2)}_{\mu}({\bf r},t)&={{1}\over{V}}\Tr[\hat{\rho}_2(t)\hat{Q}_{\mu}]\cr &={{1}\over{V}}\Tr\Big[ \underbrace{\Big(\hat{U}_0(t) \underbrace{ {{1}\over{(i\hbar)^2}}\int^t_{-\infty}\int^{\tau_1}_{-\infty} [\hat{H}'_{\rm I}(\tau_1), [\hat{H}'_{\rm I}(\tau_2),\hat{\rho}_0]]\,d\tau_2\,d\tau_1 }_{=\hat{\rho}'_2(t){\quad\hbox{\ninerm(interaction picture)}}} \hat{U}_0(-t)\Big) }_{=\hat{\rho}_2(t){\quad\hbox{\ninerm(Schroedinger picture)}}} \hat{Q}_{\mu}\Big]\cr &=\{E_{\alpha}(\tau_1){\rm\ and\ }E_{\alpha}(\tau_1) {\rm\ are\ classical\ fields\ (omit\ space\ dependence\ {\bf r})}\}\cr &={{1}\over{V(i\hbar)^2}}\Tr\Big\{ \hat{U}_0(t)\int^t_{-\infty}\int^{\tau_1}_{-\infty} [\hat{Q}_{\alpha}(\tau_1), [\hat{Q}_{\beta}(\tau_2),\hat{\rho}_0]] E_{\alpha}(\tau_1) E_{\beta}(\tau_2)\,d\tau_2\,d\tau_1 \hat{U}_0(-t)\,\hat{Q}_{\mu}\Big\}\cr &=\{{\rm Pull\ out\ }E_{\alpha_1}(\tau_1) E_{\alpha_2}(\tau_2) {\rm\ and\ the\ integrals\ outside\ the\ trace}\}\cr }$

$\eqalign{ &={{1}\over{V(i\hbar)^2}}\int^t_{-\infty}\int^{\tau_1}_{-\infty} \Tr\Big\{\hat{U}_0(t) [\hat{Q}_{\alpha}(\tau_1),[\hat{Q}_{\beta}(\tau_2),\hat{\rho}_0]] \hat{U}_0(-t)\,\hat{Q}_{\mu}\Big\} E_{\alpha}(\tau_1) E_{\beta}(\tau_2)\,d\tau_2\,d\tau_1.\cr }$

In analogy with the results as obtained for the first order (linear) optical properties, now express the term E_α₁(τ₁)E_α₂(τ₂) in the frequency domain, by using the Fourier identity

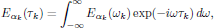
$E_{\alpha_k}(\tau_k)=\int^{\infty}_{-\infty} E_{\alpha_k}(\omega_k)\exp(-i\omega\tau_k)\,d\omega,$

which hence gives the second order polarization density expressed in terms of the electric field in the frequency domain as

$\eqalign{ P^{(2)}_{\mu}({\bf r},t) &={{1}\over{V(i\hbar)^2}}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} \int^t_{-\infty}\int^{\tau_1}_{-\infty} \Tr\Big\{\hat{U}_0(t) [\hat{Q}_{\alpha}(\tau_1),[\hat{Q}_{\beta}(\tau_2),\hat{\rho}_0]] \hat{U}_0(-t)\,\hat{Q}_{\mu}\Big\} E_{\alpha}(\omega_1) E_{\beta}(\omega_2) \cr&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\times \exp(-i\omega_1\tau_1)\exp(-i\omega_2\tau_2) \,d\tau_2\,d\tau_1\,d\omega_2\,d\omega_1\cr &=\{{\rm Use\ }\exp(-i\omega\tau)=\exp(-i\omega t) \exp[-i\omega(\tau-t)]\}\cr &={{1}\over{V(i\hbar)^2}}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} \int^t_{-\infty}\int^{\tau_1}_{-\infty} \Tr\Big\{\hat{U}_0(t) [\hat{Q}_{\alpha}(\tau_1),[\hat{Q}_{\beta}(\tau_2),\hat{\rho}_0]] \hat{U}_0(-t)\,\hat{Q}_{\mu}\Big\} E_{\alpha}(\omega_1) E_{\beta}(\omega_2) \cr&\qquad\qquad\qquad\qquad\times \exp[-i\omega_1(\tau_1-t)-i\omega_2(\tau_2-t)] \,d\tau_2\,d\tau_1\,\exp[-i\underbrace{(\omega_1+\omega_2)}_{ =\omega_{\sigma}}t] \,d\omega_2\,d\omega_1\cr &=\varepsilon_0\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} \chi^{(2)}_{\mu\alpha\beta}(-\omega_{\sigma};\omega_1,\omega_2) E_{\alpha}(\omega_1) E_{\beta}(\omega_2) \exp(-i\omega_{\sigma} t)\,d\omega_2\,d\omega_1,\cr }$

where the second order (quadratic) electric susceptibility is defined as

$\eqalign{ \chi^{(2)}_{\mu\alpha\beta}&(-\omega_{\sigma};\omega_1,\omega_2)\cr &={{1}\over{\varepsilon_0 V(i\hbar)^2}} \int^t_{-\infty}\int^{\tau_1}_{-\infty} \Tr\Big\{\hat{U}_0(t) [\hat{Q}_{\alpha}(\tau_1),[\hat{Q}_{\beta}(\tau_2),\hat{\rho}_0]] \hat{U}_0(-t)\,\hat{Q}_{\mu}\Big\} \cr&\qquad\qquad\qquad\qquad\times \exp[-i\omega_1(\tau_1-t)-i\omega_2(\tau_2-t)] \,d\tau_2\,d\tau_1\cr &=\{{\rm Make\ use\ of\ Eq.\ (2)\ and\ take\ }\tau'_1=\tau_1-t\}\cr &=\ldots\cr &={{1}\over{\varepsilon_0 V(i\hbar)^2}} \int^0_{-\infty}\int^{\tau'_1}_{-\infty} \Tr\{\hat{\rho}_0[[\hat{Q}_{\mu},\hat{Q}_{\alpha}(\tau'_1)], \hat{Q}_{\beta}(\tau'_2)]\} \exp[-i(\omega_1\tau'_1+\omega_2\tau'_2)] \,d\tau'_2\,d\tau'_1.\cr }$

This obtained expression for the second order electric susceptibility does not possess the property of intrinsic permutation symmetry. However, by using the same arguments as discussed in the analysis of the polarization response functions in lecture two, we can easily verify that this tensor can be cast into a symmetric and antisymmetric part as

$\eqalign{ \chi^{(2)}_{\mu\alpha\beta}(-\omega_{\sigma};\omega_1,\omega_2) &={{1}\over{2}}\underbrace{[ \chi^{(2)}_{\mu\alpha\beta}(-\omega_{\sigma};\omega_1,\omega_2) +\chi^{(2)}_{\mu\beta\alpha}(-\omega_{\sigma};\omega_2,\omega_1)]}_{ {\rm symmetric\ part}} \cr&\qquad\qquad +{{1}\over{2}}\underbrace{[ \chi^{(2)}_{\mu\alpha\beta}(-\omega_{\sigma};\omega_1,\omega_2) -\chi^{(2)}_{\mu\beta\alpha}(-\omega_{\sigma};\omega_2,\omega_1)]}_{ {\rm antisymmetric\ part}},\cr }$

and since the antisymmetric part, again following the arguments for the second order polarization response function, does not contribute to the polarization density, it is customary (in the Butcher and Cotter convention as well as all other conventions in nonlinear optics) to cast the second order susceptibility into the form

$\eqalign{ \chi^{(2)}_{\mu\alpha\beta}&(-\omega_{\sigma};\omega_1,\omega_2)\cr &={{1}\over{\varepsilon_0 V(i\hbar)^2}}{{1}\over{2!}}{\bf S} \int^0_{-\infty}\int^{\tau'_1}_{-\infty} \Tr\{\hat{\rho}_0[[\hat{Q}_{\mu},\hat{Q}_{\alpha}(\tau'_1)], \hat{Q}_{\beta}(\tau'_2)]\} \exp[-i(\omega_1\tau'_1+\omega_2\tau'_2)] \,d\tau'_2\,d\tau'_1,\cr }$

where S, commonly called the symmetrizing operator, denotes that the expression that follows is to be summed over the 2! = 2 possible pairwise permutations of (α, ω₁) and (β, ω₁), hence ensuring that the second order susceptibility possesses the intrinsic permutation symmetry,

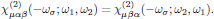
$\chi^{(2)}_{\mu\alpha\beta}(-\omega_{\sigma};\omega_1,\omega_2) =\chi^{(2)}_{\mu\beta\alpha}(-\omega_{\sigma};\omega_2,\omega_1).$

2. Higher order polarization densities

The previously described principle of deriving the susceptibilities of first and second order are straightforward to extend to the n:th order interaction. In this case, we will make use of the following generalization of Eq. (2),

$\eqalign{ \Tr\{[&\hat{Q}_{\alpha_1}(\tau_1),[\hat{Q}_{\alpha_2}(\tau_2),\ldots, [\hat{Q}_{\alpha_n}(\tau_n),\hat{\rho}_0]]\ldots]\hat{Q}_{\mu}\}\cr &\qquad=\Tr\{\hat{\rho}_0[\ldots[[\hat{Q}_{\mu},\hat{Q}_{\alpha_1}(\tau_1)], \hat{Q}_{\alpha_2}(\tau_2)],\ldots\hat{Q}_{\alpha_n}(\tau_n)]\},\cr }$

which, when applied in the evaluation of the expectation value of the electric dipole operator of the ensemble, gives the n:th order electric susceptibility as

$\eqalign{ \chi^{(n)}_{\mu\alpha_1\cdots\alpha_n} &(-\omega_{\sigma};\omega_1,\ldots,\omega_n)\cr &={{1}\over{\varepsilon_0 V (-i\hbar)^n}}{{1}\over{n!}}{\bf S} \int^0_{-\infty}\int^{\tau_1}_{-\infty}\cdots\int^{\tau_{n-1}}_{-\infty} \Tr\{\hat{\rho}_0[\ldots[[\hat{Q}_{\mu},\hat{Q}_{\alpha_1}(\tau_1)], \hat{Q}_{\alpha_2}(\tau_2)],\ldots\hat{Q}_{\alpha_n}(\tau_n)]\} \cr&\qquad\qquad\qquad\qquad\qquad\qquad\times \exp[-i(\omega_1\tau_1+\omega_2\tau_2+\ldots+\omega_n\tau_n)] \,d\tau_n\,\cdots\,d\tau_2\,d\tau_1,\cr }$

where now the symmetrizing operator S indicates that the expression following it should be summed over all the n! pairwise permutations of (α₁,ω₁), … , (α_n, ω_n)$.

It should be emphasized the symmetrizing operator S always implies summation over all the n! pairwise permutations of (α₁,ω₁), … , (α_n, ω_n)$, regardless of whether the permutations are distinct or not. This is due to that eventually occuring degenerate permutations are taken care of in the degeneracy coefficient K(-ω_σ; ω₁, …, ω_n) in Butcher and Cotters convention, as described in lecture three and in the additional notes which were handed out during lecture four.

References

[1] It should be noticed that the form given in Eq. (1) not only applies to an ensemble of molecules, of arbitrary composition, but also to any kind of level of approximation for the interaction, such as the inclusion of magnetic dipolar interactions or electric quadrupolar interactions as well. These interactions should (of course) be incorporated in the expression for the interaction Hamiltonian 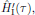$\hat{H}'_{\rm I}(\tau)$ , here described in the interaction picture.