Volume 97, Number 19, 193903 (November 2006).
Photospin-Orbit Coupling in Photonic Structures
Fredrik Jonsson1 and Christos Flytzanis2
1EPSRC Nanophotonics Portfolio Centre, School of Physics and Astronomy, University of Southampton, SO17 1BJ, United Kingdom.2Laboratoire Pierre Aigrain, Ecole Normale Superieure, 24 rue Lhomond, 75231-Paris Cedex 05, France.
Abstract
We show that inclusion of non-locality in the constitutive relations in photonic structures has important repercussions in their eigenmode configuration and distribution. In the case of optical activity, the primary manifestation of non-locality, these features are traced to a photospin-orbit interaction analogous to the electron spin-orbit interaction in asymmetric semiconducting compounds; its impact can be assimilated to that of a magnetic field whose magnitude and direction follows that of the photon quasi-momentum, with implications in photospin transport and photo-spintronics.
Full text: PDF [250 kB] | DOI: 10.1103/PhysRevLett.97.193903
This article was featured in the November 20th (2006) issue of Virtual Journal of Nanoscale Science and Technology, published by the American Institute of Physics and the American Physical Society.
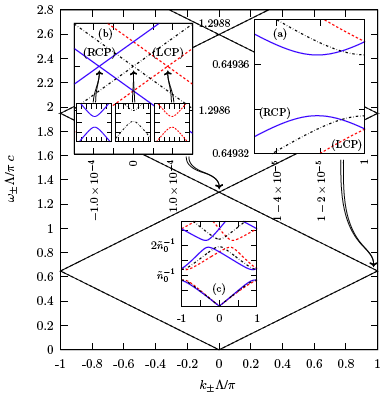
Figure 1. The dispersion relations ω−(k−) of right (solid) and ω+(k+) of left (dashed) circularly polarized modes propagating in an infinite periodic and optically active medium. The limiting band diagram in the absence of rotatory power is shown as dot-dashed curves. The insets show enlargements of the (a) first and (b) second order band gaps, in which the wave-vector splitting of the circular polarization states is manifested as an asymmetry in the band diagram. Parameter values were taken as those for crystalline quartz of trigonal point symmetry group 32, which at a vacuum wavelength of 633 nm possesses a refractive index of n0 = ε1/20 = 1.54 and a rotatory power of 19.0 deg/mm, or α0K = 2.1×10-4, with a spatial bottom-to-peak index modulation of 2.7×10-5 (ε±1 = 1.0×10-4) and α±1 = α0/10. The grating period was chosen as Λ = 206 nm, corresponding to a first-order Bragg resonance at 633 nm vacuum wavelength. The wave-vector splitting of the second-order bandgap is k+-k- = 1.7×10-4π/Λ = 26 cm-1. For visual clarity, inset (c) shows the corresponding band diagram with parameters ε±1 and α0 greatly exaggerated.