Lectures on Nonlinear Optics - Lecture 4
Quantum mechanics I: Formulation of linear optical interactions
lect4.pdf [283 kB] Lecture 4 in Portable Document Format.
Contents
- The Truth of polarization densitites
- Outline
- Quantum mechanics
- Perturbation analysis of the density operator
- The interaction picture
- The first order polarization density
1. The Truth of polarization densitites
So far, we have performed the analysis in a theoretical framework that has been exclusively formulated in terms of phenomenological models, such as the anharmonic oscillator and the phenomenologically introduced polarization response function of the medium. In the real world application of nonlinear optics, however, we should not restrict the theory just to phenomenological models, but rather take advantage over the full quantum-mechanical framework of analysis of interaction between light and matter.
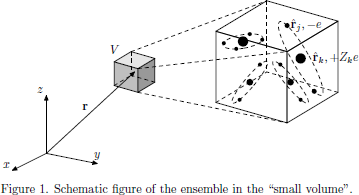
In a small volume V (smaller than the wavelength of the light, to ensure that the natural spatial variation of the light is not taken into account, but large enough in order to contain a sufficcient number of molecules in order to ignore the quantum-mechanical fluctuations of the dipole moment density), we consider the applied electric field to be homogeneous, and the electric polarization density of the medium is then given as the expectation value of the electric dipole operator of the ensemble of molecules divided by the volume, as
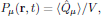 (1)
(1)where the electric dipole operator of the ensemble contained in V can be written as a sum over all electrons and nuclei as
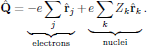 (2)
(2)
The expectation value
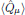 of the μ-component (for
simplicity, we here stick to this being the component along the Cartesian
eμ-axes) of the vectorial operator can in principle be
calculated directly from the compound, time-dependent wave function of
the ensemble of molecules in the small volume, considering any kind of
interaction between the molecules, which may be of an arbitrary composition.
However, we will here describe the interactions that take place in terms
of the quantum mechanical density operator of the ensemble, in which
case the expectation value is calculated from the quantum mechanical
trace as
of the μ-component (for
simplicity, we here stick to this being the component along the Cartesian
eμ-axes) of the vectorial operator can in principle be
calculated directly from the compound, time-dependent wave function of
the ensemble of molecules in the small volume, considering any kind of
interaction between the molecules, which may be of an arbitrary composition.
However, we will here describe the interactions that take place in terms
of the quantum mechanical density operator of the ensemble, in which
case the expectation value is calculated from the quantum mechanical
trace as
![$$
P_{\mu}({\bf r},t)=\Tr[\hat{\rho}(t)\hat{Q}_{\mu}]/V.
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_003.png) (3)
(3)2. Outline
Previously, in lecture one, we applied the mathematical tool of perturbation analysis to a classical mechanical model of the dipole moment. This analysis will now essentially be repeated, but now we will instead consider a perturbation series for the quantum mechanical density operator, with the series being of the form
![$$
\hat{\rho}(t)=\underbrace{\hat{\rho}_0}_{\sim [E(t)]^0}
+\underbrace{\hat{\rho}_1(t)}_{\sim [E(t)]^1}
+\underbrace{\hat{\rho}_2(t)}_{\sim [E(t)]^2}
+\ldots
+\underbrace{\hat{\rho}_n(t)}_{\sim [E(t)]^n}
+\ldots
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_004.png) (4)
(4)As this perturbation series is inserted into the expression for the electric polarization density, we will obtain a resulting series for the polarization density as
![$$
P_{\mu}({\bf r},t)=\sum^{\infty}_{m=0}\underbrace{\Tr[\hat{\rho}_m(t)
\hat{Q}_{\mu}]/V}_{=P^{(m)}_{\mu}({\bf r},t)}
\approx\sum^{n}_{m=0} P^{(m)}_{\mu}({\bf r},t).
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_005.png) (5)
(5)It is the aim of the current lecture to illustrate how this (rather simple) principle of perturbation in a straightforward way can be employed to the formulation of a quantum-mechanical framework for nonlinear optical interactions.
3. Quantum mechanics
We consider an ensemble of molecules, where each molecule may be different from the other molecules of the ensemble, as well as being affected by some mutual interaction between the other members of the ensemble. The Hamiltonian for this ensemble is generally taken as
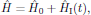 (6)
(6)
where
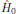 is the Hamiltonian at thermal equilibrium, with no
external forces (or sources) present, and
is the Hamiltonian at thermal equilibrium, with no
external forces (or sources) present, and
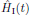 is the interaction
Hamiltonian (in the so-called Schrödinger picture; more about
this later on when we arrive at the
interaction picture), which for electric dipolar interactions take the
form:
is the interaction
Hamiltonian (in the so-called Schrödinger picture; more about
this later on when we arrive at the
interaction picture), which for electric dipolar interactions take the
form:
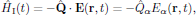 (7)
(7)
where
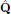 is the electric dipole operator of the
ensemble of molecules contained in the small volume V
(see Fig. 1). This expression
may be compared with the all-classical electrostatic energy of an electric
dipole moment in a electric field,
is the electric dipole operator of the
ensemble of molecules contained in the small volume V
(see Fig. 1). This expression
may be compared with the all-classical electrostatic energy of an electric
dipole moment in a electric field,
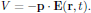
In order to provide a proper description of the interaction between light and matter at molecular level, we must be means of some quantum mechanical description evaluate all properties of the molecule, such as electric dipole moment, magnetic dipole moment, etc., by means of quantum mechanical expectation values.
The description that we here will apply is by means of the density operator formalism, with the density operator defined in terms of orthonormal set of wave functions |a> of the system as
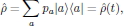 (8)
(8)where pa are the normalized probabilities of the system to be in state |a>, with
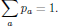 (9)
(9)From the density operator, the expectation value of any arbitrary quantum mechanical operator $\hat{O}$ of the ensemble is obtained from the quantum mechanical trace as
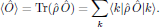 (10)
(10)The equation of motion for the density operator is given in terms of the Hamiltonian as
![$$
\eqalign{
i\hbar{{d\hat{\rho}}\over{dt}}
&=[\hat{H},\hat{\rho}]
=\hat{H}\hat{\rho}-\hat{\rho}\hat{H}\cr
&=[\hat{H}_0,\hat{\rho}]+[\hat{H}_{\rm I}(t),\hat{\rho}]\cr
}
\eqno{(1)}
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_012.png) (11)
(11)In this context, the terminology of "equation of motion" can be pictured as
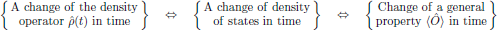
Whenever external forces are absent, that is to say, whenever the applied electromagnetic field is zero, the equation of motion for the density operator takes the form
![$$i\hbar{{d\hat{\rho}}\over{dt}}=[\hat{H}_0,\hat{\rho}],$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_014.png) (12)
(12)with the solution [1]
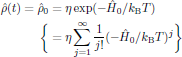 (13)
(13)being the time-independent density operator at thermal equilibrium, with the normalization constant η chosen so that
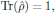
that is to say, with the normalization constant η chosen as
![$$\eta=1/\Tr[\exp(-\hat{H}_0/k_{\rm B}T)].$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_017.png)
4. Perturbation analysis of the density operator
The task is now o obtain a solution of the equation of motion (11) by means of a perturbation series, in similar to the analysis performed for the anharmonic oscillator in the first lecture of this course. The perturbation series is, in analogy to the mechanical spring oscillator under influence of an electromagnetic field, taken as
![$$
\hat{\rho}(t)=\underbrace{\hat{\rho}_0}_{\sim [E(t)]^0}
+\underbrace{\hat{\rho}_1(t)}_{\sim [E(t)]^1}
+\underbrace{\hat{\rho}_2(t)}_{\sim [E(t)]^2}
+\ldots
+\underbrace{\hat{\rho}_n(t)}_{\sim [E(t)]^n}
+\ldots
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_018.png)
The boundary condition of the perturbation series is taken as the initial condition that sometime in the past, the external forces has been absent, that is to say
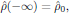
which, since the perturbation series is to be valid for all possible evolutions in time of the externally applied electric field, leads to the boundary conditions for each individual term of the perturbation series as

By inserting the perturbation series for the density operator into the equation of motion (11), one hence obtains
![$$
\eqalign{
i\hbar{{d}\over{dt}}(\hat{\rho}_0+\hat{\rho}_1(t)+\hat{\rho}_2(t)
+\ldots+\hat{\rho}_n(t)+\ldots)
&=[\hat{H}_0,\hat{\rho}_0+\hat{\rho}_1(t)+\hat{\rho}_2(t)
+\ldots+\hat{\rho}_n(t)+\ldots]\cr
&\qquad+[\hat{H}_{\rm I}(t),\hat{\rho}_0+\hat{\rho}_1(t)+\hat{\rho}_2(t)
+\ldots+\hat{\rho}_n(t)+\ldots],\cr
}
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_021.png)
and by equating terms with equal power dependence of the applied electric field in the right and left hand sides, one obtains the system of equations
![$$
\eqalign{
i\hbar{{d\hat{\rho}_0}\over{dt}}&=[\hat{H}_0,\hat{\rho}_0],\cr
i\hbar{{d\hat{\rho}_1(t)}\over{dt}}&=[\hat{H}_0,\hat{\rho}_1(t)]
+[\hat{H}_{\rm I}(t),\hat{\rho}_0],\cr
i\hbar{{d\hat{\rho}_2(t)}\over{dt}}&=[\hat{H}_0,\hat{\rho}_2(t)]
+[\hat{H}_{\rm I}(t),\hat{\rho}_1(t)],\cr
&\vdots\cr
i\hbar{{d\hat{\rho}_n(t)}\over{dt}}&=[\hat{H}_0,\hat{\rho}_n(t)]
+[\hat{H}_{\rm I}(t),\hat{\rho}_{n-1}(t)],\cr
&\vdots\cr
}\eqno{(2)}
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_024.png) (14)
(14)
for the variuos order terms of the perturbation series. In Eq. (14), we may
immediately notice that the first equation simply is the identity stating
the thermal equilibrium condition for the zeroth order term
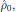 while all other terms may be obtained by consecutively solve the equations
of order j = 1, 2, …, n, in that order.
while all other terms may be obtained by consecutively solve the equations
of order j = 1, 2, …, n, in that order.
5. The interaction picture
We will now turn our attention to the problem of actually solving the obtained system of equations for the terms of the perturbation series for the density operator. In a classical picture, the obtained equations are all of the form similar to
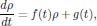 (15)
(15)for known functions f(t) and g(t). To solve such an equation, just applying standard textbook techniques in calculus, we generally look for an integrating factor I(t) satisfying
![$$
I(t){{d\rho}\over{dt}}-I(t)f(t)\rho={{d}\over{dt}}[I(t)\rho].\eqno{(4)}
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_026.png) (16)
(16)By carrying out the differentiation in the right hand side of the equation, we find that the integrating factor should satisfy
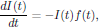
which is solved by
![$$
I(t)=I(0)\exp\big[-\int^t_0 f(\tau)\,d\tau\big].
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_028.png)
(Butcher and Cotter have in their classical description of integrating factors chosen to put I(0) = 1.)
The original ordinary differential equation (15) is hence solved by multiplying with the intagrating factor I(t) and using the property (16) of the integrating factor, giving the equation
![$$
{{d}\over{dt}}[I(t)\rho]=I(t)g(t),
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_029.png)
from which we hence obtain the solution for ρ(t) as
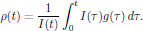
From this preliminary discussion we may anticipate that equations of motion for the various order perturbation terms of the density operator can be solved in a similar manner, using integrating factors. However, it should be kept in mind that we here are dealing with operators and not classical quantities, and since we do not know if the integrating factor is to be multiplied from left or right.
In order not to loose any generality, we may look for a set of two
integrating factors
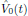 and
and
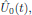 in operator sense,
that we left and right multiply the unknown terms of the n:th order
equation by, and we require these operators to have the effective impact
in operator sense,
that we left and right multiply the unknown terms of the n:th order
equation by, and we require these operators to have the effective impact
![$$
\hat{V}_0(t)\bigg\{i\hbar{{d\hat{\rho}_n(t)}\over{dt}}
-[\hat{H}_0,\hat{\rho}_n(t)]\bigg\}\hat{U}_0(t)
=i\hbar{{d}\over{dt}}[\hat{V}_0(t)\hat{\rho}_n(t)\hat{U}_0(t)].
\eqno{(5)}
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_031.png) (17)
(17)By carrying out the differentiation in the right-hand side, expanding the commutator in the left hand side, and rearranging terms, one then obtains the equation
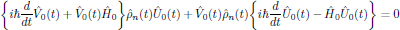
for the operators
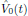 and
and
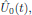 . This equation clearly
is satisfied if both of the braced expressions simultaneously are zero for
all times, in other words, if the so-called time-development operators
. This equation clearly
is satisfied if both of the braced expressions simultaneously are zero for
all times, in other words, if the so-called time-development operators
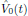 and
and
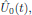 are chosen to satisfy
are chosen to satisfy
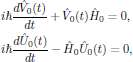 (18)
(18)with solutions
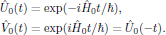
In these expressions, the exponentials are to be regarded as being defined
by their series expansion.
In particular, each term of the series expansion contains an operator part
being a power of the thermal equilibrium Hamiltonian
 , which commutes with any of the other powers.
We may easily verify that the obtained solutions, in a strict operator sense,
satisfy the relations
, which commutes with any of the other powers.
We may easily verify that the obtained solutions, in a strict operator sense,
satisfy the relations
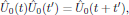
with, in particular, the corollary
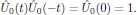
Let us now again turn our attention to the original equation of motion that was the starting point for this discussion. By multiplying the n:th order subequation of Eq. (14)with Û0(-t) from the left, and multiplying with Û0(t) from the right, we by using the relation (17) obtain
![$$
i\hbar{{d}\over{dt}}\bigg\{\hat{U}_0(-t)\hat{\rho}_n(t)\hat{U}_0(t)\bigg\}
=\hat{U}_0(-t)[\hat{H}_{\rm I}(t),\hat{\rho}_{n-1}(t)]\hat{U}_0(t),
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_037.png)
which is integrated to yield the solution
![$$
\hat{U}_0(-t)\hat{\rho}_n(t)\hat{U}_0(t)
={{1}\over{i\hbar}}\int^t_{-\infty}\hat{U}_0(-\tau)
[\hat{H}_{\rm I}(\tau),\hat{\rho}_{n-1}(\tau)]\hat{U}_0(\tau)\,d\tau,
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_038.png)
where the lower limit of integration was fixed in accordance with the initial condition
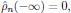
for n = 1, 2, ….
In some sense, we may consider the obtained solution as being the end point of this discussion; however, we may simplify the expression somewhat by making a few notes on the properties of the time development operators. By expanding the right hand side of the solution, and inserting
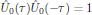
between $\hat{H}_{\rm I}(\tau)$ and $\hat{\rho}_{n-1}(\tau)$ in the two terms, we obtain
![$$
\eqalign{
\hat{U}_0(-t)\hat{\rho}_n(t)\hat{U}_0(t)
&={{1}\over{i\hbar}}\int^t_{-\infty}\hat{U}_0(-\tau)
[\hat{H}_{\rm I}(\tau)\hat{\rho}_{n-1}(\tau)
-\hat{\rho}_{n-1}(\tau)\hat{H}_{\rm I}(\tau)]\hat{U}_0(\tau)\,d\tau\cr
&={{1}\over{i\hbar}}\int^t_{-\infty}
\hat{U}_0(-\tau)\hat{H}_{\rm I}(\tau)\underbrace{\hat{U}_0(\tau)
\hat{U}_0(-\tau)}_{=1}\hat{\rho}_{n-1}(\tau)\hat{U}_0(\tau)\,d\tau\cr
&\qquad\qquad-{{1}\over{i\hbar}}\int^t_{-\infty}
\hat{U}_0(-\tau)\hat{\rho}_{n-1}(\tau)\underbrace{\hat{U}_0(\tau)
\hat{U}_0(-\tau)}_{=1}\hat{H}_{\rm I}(\tau)\hat{U}_0(\tau)\,d\tau\cr
&={{1}\over{i\hbar}}\int^t_{-\infty}
[\underbrace{\hat{U}_0(-\tau)\hat{H}_{\rm I}(\tau)\hat{U}_0(\tau)}_{
\equiv\hat{H}'_{\rm I}(t)},
\underbrace{\hat{U}_0(-\tau)\hat{\rho}_{n-1}(\tau)\hat{U}_0(\tau)}_{
\equiv\hat{\rho}'_{n-1}(t)}]\,d\tau,\cr
}
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_039.png)
and hence, by introducing the primed notation in the interaction picture for the quantum mechanical operators,
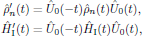
the solutions of the system of equations for the terms of the perturbation series for the density operator in the interaction picture take the simplified form
![$$
\hat{\rho}'_n(t)={{1}\over{i\hbar}}\int^t_{-\infty}
[\hat{H}'_{\rm I}(\tau),\hat{\rho}'_{n-1}(\tau)]\,d\tau,
\qquad n=1,2,\ldots,
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_041.png)
with the variuos order solutions expressed in the original Schrödinger picture by means of the inverse transformation
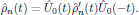
6. The first order polarization density
With the quantum mechanical perturbative description of the interaction between light and matter in fresh mind, we are now in the position of formulating the polarization density of the medium from a quantum mechanical description. A minor note should though be made regarding the Hamiltonian, which now is expressed in the interaction picture, and hence the electric dipolar operator (since the electric field here is considered to be a macroscopic, classical quantity) is given in the interaction picture as well,
![$$
\eqalign{
\hat{H}'_{\rm I}(\tau)&=\hat{U}_0(-\tau)\underbrace{
[-\hat{Q}_{\alpha}E_{\alpha}(\tau)]}_{=\hat{H}_{\rm I}(\tau)}
\hat{U}_0(\tau)\cr
&=-\hat{U}_0(-\tau)\hat{Q}_{\alpha}\hat{U}_0(\tau)E_{\alpha}(\tau)\cr
&=-\hat{Q}_{\alpha}(\tau)E_{\alpha}(\tau)\cr
}
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_043.png)
where $\hat{Q}_{\alpha}(\tau)$ denotes the electric dipolar operator of the ensemble, taken in the interaction picture.
By inserting the expression for the first order term of the perturbation series for the density operator into the quantum mechanical trace of the first order electric polarization density of the medium, one obtains
![$$
\eqalign{
P^{(1)}_{\mu}({\bf r},t)&={{1}\over{V}}\Tr[\hat{\rho}_1(t)\hat{Q}_{\mu}]\cr
&={{1}\over{V}}\Tr\Big[
\underbrace{\Big(\hat{U}_0(t)
\underbrace{{{1}\over{i\hbar}}\int^t_{-\infty}
[\hat{H}'_{\rm I}(\tau),\hat{\rho}_0]\,d\tau
}_{=\hat{\rho}'_1(t)}\hat{U}_0(-t)\Big)
}_{=\hat{\rho}_1(t)}
\hat{Q}_{\mu}\Big]\cr
&=\Bigg\{
\matrix{
E_{\mu}(\tau){\rm\ is\ a\ classical\ field
\ (omit\ space\ dependence\ {\bf r})},\cr
[\hat{H}'_{\rm I}(\tau),\hat{\rho}_0]
=[-\hat{Q}_{\alpha}(\tau)E_{\alpha}(\tau),\hat{\rho}_{0}]
=-E_{\alpha}(\tau)[\hat{Q}_{\alpha}(\tau),\hat{\rho}_{0}]
}
\Bigg\}\cr
&=-{{1}\over{V i\hbar}}\Tr\Big\{
\hat{U}_0(t)
\int^t_{-\infty} E_{\alpha}(\tau)
[\hat{Q}_{\alpha}(\tau),\hat{\rho}_0]\,d\tau\,
\hat{U}_0(-t)\,
\hat{Q}_{\mu}\Big\}\cr
&=\{{\rm Pull\ out\ }E_{\alpha}(\tau)
{\rm\ and\ the\ integral\ outside\ the\ trace}\}\cr
&=-{{1}\over{V i\hbar}}
\int^t_{-\infty} E_{\alpha}(\tau)\Tr\{
\hat{U}_0(t)[\hat{Q}_{\alpha}(\tau),\hat{\rho}_0]\hat{U}_0(-t)\,
\hat{Q}_{\mu}\}\,d\tau\cr
&=\Bigg\{{\rm Express\ }E_{\alpha}(\tau){\rm\ in\ frequency\ domain,\ }
E_{\alpha}(\tau)=\int^{\infty}_{-\infty}E_{\alpha}(\omega)
\exp(-i\omega\tau)\,d\omega\Bigg\}\cr
&=-{{1}\over{V i\hbar}}
\int^{\infty}_{-\infty} \int^t_{-\infty}
E_{\alpha}(\omega)\Tr\{
\hat{U}_0(t)[\hat{Q}_{\alpha}(\tau),\hat{\rho}_0]\hat{U}_0(-t)\,
\hat{Q}_{\mu}\}\exp(-i\omega\tau)\,d\tau\,d\omega\cr
&=\{{\rm Use\ }\exp(-i\omega\tau)=\exp(-i\omega t)
\exp[-i\omega(\tau-t)]\}\cr
&=-{{1}\over{V i\hbar}}
\int^{\infty}_{-\infty} \int^t_{-\infty}
E_{\alpha}(\omega)\Tr\{
\hat{U}_0(t)[\hat{Q}_{\alpha}(\tau),\hat{\rho}_0]\hat{U}_0(-t)\,
\hat{Q}_{\mu}\}
\cr&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\times
\exp[-i\omega(\tau-t)]\,d\tau\,\exp(-i\omega t)\,d\omega\cr
&=\varepsilon_0\int^{\infty}_{-\infty}
\chi^{(1)}_{\mu\alpha}(-\omega;\omega)E_{\alpha}(\omega)
\exp(-i\omega t)\,d\omega,\cr
}
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_045.png)
where the first order (linear) electric susceptibility is defined as
![$$
\eqalign{
\chi^{(1)}_{\mu\alpha}(-\omega;\omega)
&=-{{1}\over{\varepsilon_0 V i\hbar}}\int^t_{-\infty}
\Tr\{\underbrace{\hat{U}_0(t)[\hat{Q}_{\alpha}(\tau),\hat{\rho}_0]
\hat{U}_0(-t)}_{=[\hat{Q}_{\alpha}(\tau-t),\hat{\rho}_0]}\,
\hat{Q}_{\mu}\}\exp[-i\omega(\tau-t)]\,d\tau\cr
&=\Bigg\{\matrix{{\rm Expand\ the\ commutator\ and\ insert\ }
\hat{U}_0(-t)\hat{U}_0(t)\equiv 1\cr
{\rm\ in\ middle\ of\ each\ of\ the\ terms,\ using\ }
[\hat{U}_0(t),\hat{\rho}_0]=0\cr
\Rightarrow\hat{U}_0(t)[\hat{Q}_{\alpha}(\tau),\hat{\rho}_0]
\hat{U}_0(-t)=[\hat{Q}_{\alpha}(\tau-t),\hat{\rho}_0]}
\Bigg\}\cr
&=-{{1}\over{\varepsilon_0 V i\hbar}}\int^t_{-\infty}
\Tr\{[\hat{Q}_{\alpha}(\tau-t),\hat{\rho}_0]\hat{Q}_{\mu}\}
\exp[-i\omega(\tau-t)]\,d\tau\cr
&=\Bigg\{{\rm Change\ variable\ of\ integration\ }\tau'=\tau-t;
\int^t_{-\infty}\cdots d\tau\to\int^0_{-\infty}\cdots d\tau'\Bigg\}\cr
&=-{{1}\over{\varepsilon_0 V i\hbar}}\int^0_{-\infty}
\underbrace{\Tr\{[\hat{Q}_{\alpha}(\tau'),\hat{\rho}_0]
\hat{Q}_{\mu}\}}_{
=\Tr\{\hat{\rho}_0[\hat{Q}_{\mu},\hat{Q}_{\alpha}(\tau')]\}}
\exp(-i\omega\tau')\,d\tau'\cr
&=\{{\rm Cyclic\ permutation\ of\ the\ arguments\ in\ the\ trace}\}\cr
&=-{{1}\over{\varepsilon_0 V i\hbar}}\int^0_{-\infty}
\Tr\{\hat{\rho}_0[\hat{Q}_{\mu},\hat{Q}_{\alpha}(\tau)]\}
\exp(-i\omega\tau)\,d\tau.\cr
}
$$](/research/lectures/lect4/web/images_80proc/lect4_eq_disp_046.png)
References
[1]
For any macroscopic system,
the probability that the system is in a particular energy eigenstate
ψn, with associated energy
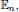 , is given by the familiar
Boltzmann distribution
, is given by the familiar
Boltzmann distribution
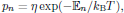
where η is a normalization constant chosen so that
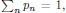
kB is the Boltzmann constant, and T the absolute temperature. This probability distribution is in this course to be considered as being an axiomatic fact, and the origin of this probability distribution can readily be obtained from textbooks on thermodynamics or statistical mechanics.