Föreläsningar i ickelinjär optik - Föreläsning 7
Spatiala symmetrier i ickelinjär optik
lect7.pdf [179 kB] Lecture 7 in Portable Document Format.
Contents
- Motivation for analysis of susceptibilities in rotated coordinate systems
- Optical properties in rotated coordinate frames
- Crystallographic point symmetry groups
- Schönflies notation for the non-cubic crystallographic point groups
- Neumann's principle
- Inversion properties
- Euler angles
- Example of the direct inspection technique applied to tetragonal media
So far, this course has mainly dealt with the dependence of the angular frequency of the light and molecular interaction strength in the description of nonlinear optics. In this lecture, we will now end this development of the description of interaction between light and matter, in favour of more engineering practical techniques for describing the theory of an experimental setup in a certain geometry, and for reducing the number of necessary tensor elements needed for describing a mediumof a certain crystallographic point-symmetry group [1].
1. Motivation for analysis of susceptibilities in rotated coordinate systems
For a given experimental setup, it is often convenient to introduce some kind of reference coordinate frame, in which one for example express the wave propagation as a linear motion along some Cartesian coordinate axis. This laboratory reference frame might be chosen, for example, with the z-axis coinciding with the direction of propagation of the optical wave at the laser output, in the phase-matched direction of an optical parametric oscillator (OPO), after some beam aligning mirror, etc.
In some cases, it might be so that this laboratory frame coincide with the natural coordinate frame of the nonlinear crystal, in which case the coordinate indices of the linear as well as nonlinear susceptibility tensors take the same values as the coordinates of the laboratory frame. (The "natural" coordinate frame of the crystal is often chosen such that some particular symmetry axis is chosen as one of the Cartesian axes.) However, we cannot generally assume the coordinate frame of the crystal to coincide with a conveniently chosen laboratory reference frame, and this implies that we generally should be prepared to spatially transform the susceptibility tensors to arbitrarily rotated coordinate frames.
Having formulated these spatial transformation rules, we will also directly benefit in another aspect of the description of nonlinear optical interactions, namely the reduction of the susceptibility tensors to the minimal set of nonzero elements. This is typically performed by using the knowledge of the so called crystallographic point symmetry group [1] of the medium, which essentially is a description of the spatial operations (rotations, inversions etc.) that define the symmetry operations of the medium.
As a particular example of the applicability of the spatial transformation rules (which we soon will formulate) is illustrated in Figs. 1 and 2. In Fig. 1, the procedure for analysis of sum or frequency difference generation is outlined. Starting from the description of the linear and nonlinear susceptibility tensors of the medium, as we previously have derived the relations from a first principle approach in Lectures 1-6, we obtain the expressions for the electric polarization densities of the medium as functions of the applied electric fields of the optical wave inside the nonlinear crystal. These polarization densities are then inserted into the wave equation, which basically is derived from Maxwell's equations of motion for the electromagnetic field. In the wave equation, the polarization densities act as source terms in an otherwise homogeneous equation for the motion of the electromagnetic field in vacuum.
As the wave equation is solved for the electric field, here taken in complex notation, we have solved for the general output from the crystal, and we can then design the experiment in such a way that an optimal efficiency is obtained.
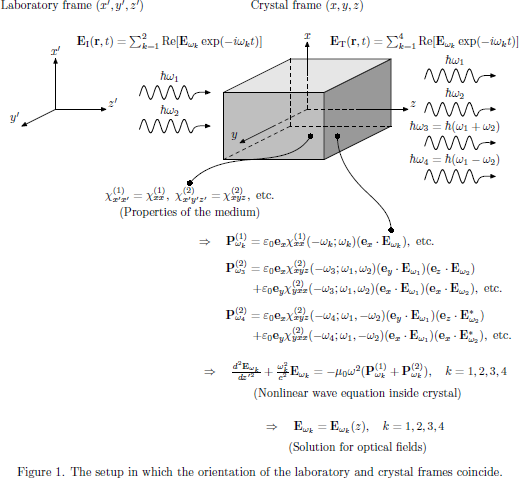
In Fig. 1, this outline is illustrated for the case where the natural coordinate frame of the crystal happens to coincide with the coordinate system of the laboratory frame. In this case, all elements of the susceptibilities taken in the coordinate frame of the crystal (which naturally is the coordinate frame in which we can obtain tabulated sets of tensor elements) will coincide with the elements as taken in the laboratory frame, and the design and interpretation of the experiment is straightforward.
However, this setup clearly constitutes a rare case, since we have infinitely many other possibilities of orienting the crystal relative the laboratory coordinate frame. Sometimes the experiment is designed with the crystal and laboratory frames coinciding, in order to simplify the interpretation of an experiment, and sometimes it is instead necessary to rotate the crytal, in order to achieve phase-matching of nonlinear process, as is the case in for example most schemes for second-order optical parametric amplification.
If now the crystal frame is rotated with respect to the laboratory frame, as shown in Fig. 2, we should make up our mind in which system we would like the wave propagation to be analyzed. In some cases, it might be so that the output of the experimental setup is most easily interpreted in the coordinate frame of the crystal, but in most cases, we have a fixed laboratory frame (fixed by the orientation of the laser, positions of mirrors, etc.) in which we would like to express the wave propagation and interaction between light and matter.
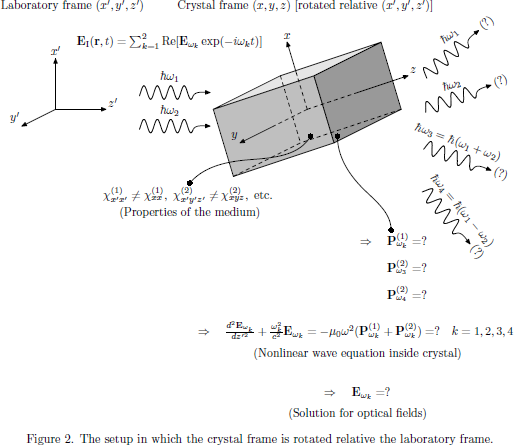
In Fig. 2, we would, in order to express the nonlinear
process in the laboratory frame, like to obtain the naturally appearing
susceptibilities
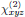 ,
,
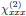 , etc., in the laboratory frame
instead, as
, etc., in the laboratory frame
instead, as
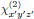 ,
,
 , etc.
, etc.
Just to summarize, why are then the transformation rules and spatial symmetries of the meduim so important?
- Hard to make physical conclusions about generated optical fields unless orientation of the laboratory and crystal frames coincide.
- Spatial symmetries often significantly simplifies the wave propagation problem (by choosing a suitable polarization state and direction of propagation of the light, etc).
- Useful for reducing the number of necessary elements of the susceptibility tensors (using Neumann's principle).
2. Optical properties in rotated coordinate frames
Consider two coordinate systems described by Cartesian coordinates xα and x'α, respectively. The coordinate systems are rotated with respect to each other, and the relation between the coordinates are described by the [3×3] transformation matrix Rab as
![$$
{\bf x}'={\bf R}{\bf x}\qquad\Leftrightarrow
\qquad x'_{\alpha}=R_{\alpha\beta}x_{\beta},
\eqno{[{\rm B.\, &\,C.}\ (5.40)]}
$$](/research/lectures/lect7/web/images_80proc/lect7_eq_disp_001.png)
where
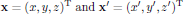
are column vectors. The inverse transformation between the coordinate systems is similarly given as
![$$
{\bf x}={\bf R}^{-1}{\bf x}'\qquad\Leftrightarrow
\qquad x_{\beta}=R_{\alpha\beta}x'_{\alpha}.
\eqno{[{\rm B.\, &\,C.}\ (5.41)]}
$$](/research/lectures/lect7/web/images_80proc/lect7_eq_disp_003.png)


We should notice that there are two types of rotations that are encountered as transformations:
- Proper rotations, for which the determinant of the rotation matrix equals to unity, det(R) = 1. (Righthanded systems keep being righthanded, and lefthanded systems keep being lefthanded.)
- Improper rotations, for which the determinant of the rotation matrix equals to minus unity, det(R) = −1. (Righthanded systems are transformed into lefthanded systems, and vice versa.)
The electric field E(r,t) and electric polarization density P(r,t) are both polar quantities that transform in the same way as regular Cartesian coordinates, and hence we have descriptions of these quantities in coordinate systems (x,y,z) and (x',y',z') related to each other as
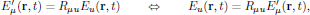
and
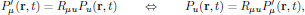
respectively. Using these transformation rules, we will now derive the form of the susceptibilities in rotated coordinate frames.
2.1. First order polarization density in rotated coordinate frames
From the transformation rule for the electric polarization density above, using the standard form as we previously have expressed the electric field dependence, we have for the first order polarization density in the primed coordinate system
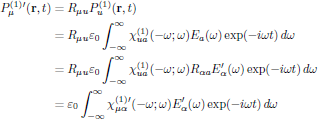
where
![$$
\chi^{(1)}_{\mu\alpha}{}'(-\omega;\omega)
=R_{\mu u}R_{\alpha a}\chi^{(1)}_{ua}(-\omega;\omega)
\eqno{[{\rm B.\, &\,C.}\ (5.45)]}
$$](/research/lectures/lect7/web/images_80proc/lect7_eq_disp_007.png)
is the linear electric susceptibility taken in the primed coordinate system.
2.2. Second order polarization density in rotated coordinate frames
Similarly, we have the second order polarization density in the primed coordinate system as
![$$
\eqalign{
P^{(2)}_{\mu}{}'({\bf r},t)
&=R_{\mu u}P^{(2)}_u({\bf r},t)\cr
&=R_{\mu u}\varepsilon_0\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}
\chi^{(2)}_{uab}(-\omega_{\sigma};\omega_1,\omega_2)
E_a(\omega_1) E_b(\omega_2)
\exp[-i(\omega_1+\omega_1)t]\,d\omega_2\,d\omega_1\cr
&=R_{\mu u}\varepsilon_0\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}
\chi^{(2)}_{uab}(-\omega_{\sigma};\omega_1,\omega_2)
R_{\alpha a} E'_{\alpha}(\omega_1)
R_{\beta b} E'_{\beta}(\omega_2)
\exp[-i(\omega_1+\omega_1)t]\,d\omega_2\,d\omega_1\cr
&=\varepsilon_0\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}
\chi^{(2)}_{\mu\alpha\beta}{}'(-\omega_{\sigma};\omega_1,\omega_2)
E'_{\alpha}(\omega_1) E'_{\beta}(\omega_2)
\exp[-i(\omega_1+\omega_1)t]\,d\omega_2\,d\omega_1\cr
}
$$](/research/lectures/lect7/web/images_80proc/lect7_eq_disp_008.png)
where
![$$
\chi^{(2)}_{\mu\alpha\beta}{}'(-\omega_{\sigma};\omega_1,\omega_2)
=R_{\mu u}R_{\alpha a}R_{\beta b}
\chi^{(2)}_{uab}(-\omega_{\sigma};\omega_1,\omega_2)
\eqno{[{\rm B.\, &\,C.}\ (5.46)]}
$$](/research/lectures/lect7/web/images_80proc/lect7_eq_disp_008.png)
is the second order electric susceptibility taken in the primed coordinate system.
2.3. Higher order polarization density in rotated coordinate frames
In a manner completely analogous to the second order susceptibility, the transformation rule between the primed and unprimed coordinate systems can be obtained for the n:th order elements of the electric susceptibility tensor as
![$$
\chi^{(n)}_{\mu\alpha_1\cdots\alpha_n}{}'
(-\omega_{\sigma};\omega_1,\ldots,\omega_n)
=R_{\mu u}R_{\alpha_1 a_1}\cdots R_{\alpha_n a_n}
\chi^{(n)}_{u a_1\cdots a_n}(-\omega_{\sigma};\omega_1,\ldots,\omega_n).
\eqno{[{\rm B.\, &\,C.}\ (5.47)]}
$$](/research/lectures/lect7/web/images_80proc/lect7_eq_disp_008.png)
3. Crystallographic point symmetry groups
Typically, a particular point symmetry group of the medium can be described by the generating matrices that describe the minimal set of transformation matrices (describing a set of symmetry operations) that will be necessary for the reduction of the constitutive tensors. Two systems are widely used for the description of point symmetry groups [2]:
- The International system.
Examples of notation:
 ,
,
 ,
,
 , etc.
, etc. - The Schönflies system. Examples of notation: Td, Oh, D4, etc.
The crystallographic point symmetry groups may contain any of the following symmetry operations:
-
Rotations through integral multiples of 2π/n about some axis.
The axis is called the n-fold rotation axis. It is in solid state physics shown (see Refs. [1-3]) that a Bravais lattice can contain only 2-, 3-, 4-, or 6-fold axes, and since the crystallographic point symmetry groups are contained in the Bravais lattice point groups, they too can only have these axes. -
Rotation-reflections.
Even when a rotation through 2π/n is not a symmetry element, sometimes such a rotation followed by a reflection in a plane perpendicular to the axis may be a symmetry operation. The axis is then called an n-fold rotation-reflection axis. For example, the groups S6 and S4 have 6- and 4-fold rotation-reflection axes, respectively. -
Rotation-inversions.
Similarly, sometimes a rotation through 2π/n followed by an inversion in a point lying on the rotation axis is a symmetry element, even though such a rotation by itself is not. The axis is then called an n-fold rotation-inversion axis. However, the axis in S6 is only a 3-fold rotation-inversion axis. -
Reflections.
A reflection takes every point into its mirror image in a plane, known as a mirror plane. -
Inversions.
An inversion has a single fixed point. If that point is taken as the origin, then every other point r is taken into −r.
4. Schönflies notation for the non-cubic crystallographic point groups
The twenty-seven non-cubic crystallographic point symmetry groups may contain any of the following symmetry operations, here given in Schönflies notation [3]:
| Cn | These groups contain only an n-fold rotation axis. |
| Cnv | In addition to the n-fold rotation axis, these groups have a mirror plane that contains the axis of rotation, plus as many additional mirror planes as the existence of the n-fold axis requires. |
| Cnh | In addition to the n-fold rotation axis, these groups contain a single mirror plane that is perpendicular to the axis. |
| Sn | These groups contain only an n-fold rotation-reflection axis. |
| Dn | In addition to the n-fold rotation axis, these groups contain a 2-fold axis perpendicular to the n-fold rotation axis, plus as many additional 2-fold axes as are required by the existence of the n-fold axis. |
| Dnh | These (the most symmetric groups) contain all the elements of Dn plus a mirror plane perpendicular to the n-fold axis. |
| Dnd | These contain the elements of Dn plus mirror planes containing the n-fold axis, which bisect the angles between the 2-fold axes. |
5. Neumann's principle
Neumann's principle simply states that any type of symmetry which is exhibited by the point symmetry group of the medium is also possessed by every physical property of the medium.
In other words, we can reformulate this for the optical properties as: the susceptibility tensors of the medium must be left invariant under any transformation that also is a point symmetry operation of the medium, or
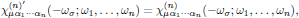
where the tensor elements in the primed coordinate system are transformed according to

where the [3×3] matrix R describes a point symmetry operation of the system.
6. Inversion properties
If the coordinate inversion, Rαβ = −δαβ, is a symmetry operation of the medium (that is to say, if the medium possess inversion symmetry), then it turns out that
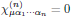
for all even numbers n.
(Question: Is this operation a proper or an improper rotation? Answer: This is an improper rotation, since the determinant of the rotation matrix is negative, det(R) = (−1)3 = −1.)
7. Euler angles
As a convenient way of expressing the matrix of proper rotations, one may use the Euler angles of classical mechanics [4],
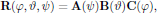
where

8. Example of the direct inspection technique applied to tetragonal media
Neumann's principle provides a highly useful methodology, with applications in a wide range of disciplines in physics and engineering. In order to illustrate this, we will now apply Neumann's principle to a particular problem, namely the reduction of the number of elements of the second order electric susceptibility tensor, in a tetragonal medium belonging to point symmetry group 422.

By inspecting Tables 2 and 3 of Hartmann's An introduction to Crystal Physics [2], one finds that the point symmetry group 422 of tetragonal media is described by the generating matrices
![$$
{\bf M}_4=\pmatrix{1&0&0\cr 0&-1&0\cr 0&0&-1},\qquad
\left[\matrix{{\rm twofold\ rotation}\cr{\rm about\ }x_1{\rm\ axis}}\right]
$$](/research/lectures/lect7/web/images_80proc/lect7_eq_disp_017.png)
and
![$$
{\bf M}_7=\pmatrix{0&-1&0\cr 1&0&0\cr 0&0&1}.\qquad
\left[\matrix{{\rm fourfold\ rotation}\cr{\rm about\ }x_3{\rm\ axis}}\right]
$$](/research/lectures/lect7/web/images_80proc/lect7_eq_disp_018.png)
8.1. Does the 422 point symmetry group possess inversion symmetry?
In Fig. 6, the steps involved for transformation of the object into an inverted coordinate frame are shown.

The result of the sequence in Fig. 6 is an object which cannot be reoriented in such a way that one obtains the same shape as we started with for the non-inverted coordinate system, and hence the object of point symmetry group 422 does not possess inversion symmetry.
8.2. Step one - Point symmetry under twofold rotation around the x1-axis
Considering the point symmetry imposed by the R = M4 matrix, we find that (for simplicity omitting the frequency arguments of the susceptibility tensor) the second order susceptibility in the rotated coordinate frame is described by the diagonal elements

and

which, by noticing that the similar form R3α = −δ3α holds for the 333-component (that is to say, the zzz-component), also gives χ333 = −χ333 = =0 . Furthermore, we for the 231-component have
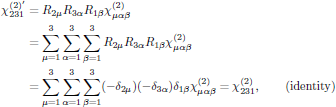
etc., and by continuing in this manner for all 27 elements of
 ,
one finds that the symmetry operation
R = M4 leaves us with the tensor
elements listed in Table 1.
,
one finds that the symmetry operation
R = M4 leaves us with the tensor
elements listed in Table 1.

8.3. Step two - Point symmetry under fourfold rotation around the x3-axis
Proceeding with the next point symmetry operation, described by R = M7, one finds for the remaining 13 elements that, for example, for the 123-element

and for the 132-element

while the 111-element (which previously, by using the R = M4 point symmetry, just gave an identity with no further information) now gives
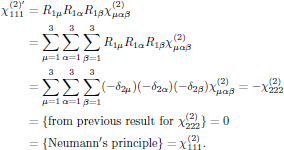
By (again) proceeding for all 27 elements of
 ,
one finds the set of tensor elements as listed in Table 2
[5].
,
one finds the set of tensor elements as listed in Table 2
[5].

References
[1] For an informal and illustrative discussion on group symmetry applied in a general and molecular context, see for example the Wikipedia articles on Symmetry groups and Molecular_symmetries.
[2] C. f. Table 2 of Ervin Hartmann, An Introduction to Crystal Physics (International Union of Crystallography, University College Cardiff, 1984); Electronic edition 2001. ISBN 0-906449-72-3. Please notice that there is a printing error in Table 3, where the twofold rotation about the x3-axis should be described by a matrix denoted "M2", and not "M1", as the table states. Download [2.77 MB]
[3] In Schönflies notation, C stands for "cyclic", D for "dihedral", and S for "spiegel". The subscripts h, v, and d stand for "horizontal", "vertical", and "diagonal", respectively, and refer to the placement of the placement of the mirror planes with respect to the n-fold axis, always considered to be vertical. (Example: The "diagonal" planes in Dnd are vertical and bisect the angles between the 2-fold axes).
[4] Herbert Goldstein, Classical Mechanics, (Addison-Wesley, London, 1980).
[5] See also the tabulated set in Butcher and Cotter's book, Table A3.2, page 299.