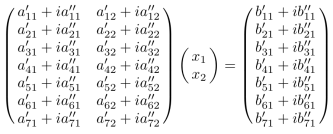zgaussj.f
The ZGAUSSJ(A,N,NP,B,M,MP) routine solves the complex-valued system of linear equations Ax = B by Gauss-Jordan elimination. The employed algorithm is similar to the one as used in Eq. (2.1.1) of Numerical Recipes in Fortran 77 [1], but here modified to solve complex-valued systems. Here A(1:N,1:N) is the input system matrix A stored in an array of dimensions NP by NP, while B(1:N,1:M) is an input matrix containing the M right-hand side vectors B, stored in an array of dimensions NP by MP.
On return, A(1:N,1:N) is replaced by its matrix inverse, and B(1:N,1:M) is replaced by the corresponding set of solution vectors. The parameter NMAX contains the largest anticipated value of N.
An example of usage of the zgaussj(a,z) routine can be found in the enclosed driver, zgaussjdrv.f.
Source files
zgaussj.f
[4 kB]
Fortran 77 source for the zgaussj(a,z) routine.
[ download |
view source ]
zgaussjdrv.f [4 kB] Fortran 77 source for the driver of the zgaussj(a,z) routine, illustrating its use for the special case of a system matrix A taken as
A11 = 1.4 + i3.3,
A12 = -2.3 + i1.7,
A13 = 2.1 + i2.9,
A21 = -3.4 + i2.3,
A22 = 1.3 - i1.7,
A23 = -3.2 - i1.4,
A31 = 1.3 - i2.3,
A32 = 2.8 + i1.1,
A33 = -1.7 - i1.2,
and a right-hand side B taken as the vector
B11 = B1 = 1.3,
B21 = B2 = -2.1,
B31 = B3 = 0.7.
Compile the Fortran-77 code for the driver using g77 [2]
and the enclosed Makefile.
[ download |
view source ]
Makefile [11 kB]
The Makefile for compilation of the driver for the zgaussj(a,z) routine.
To compile the source file into an executable, simply run 'make' in the
directory containing
zgaussj.f and
zgaussjdrv.f.
[ download |
view source ]
References
[1] W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in Fortran 77, The Art of Scientific Computing, 2nd edition (Cambridge University Press, Cambridge, 1992). http://www.nr.com/
[2] Documentation for the GNU Fortran 77 compiler, commonly denoted g77, is available online at http://gcc.gnu.org/onlinedocs/g77/.