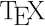Summary | Source | Compilation | Precompiled | Execution | Gallery | References
Wiener
The WIENER program computes a series of floating-point numbers corresponding to a Wiener process in D dimensions. The program relies on the random number generator as proposed by Donald Knuth in The Art of Computer Programming, Volume 1 – Fundamental Algorithms, 3rd edition (Addison-Wesley, Boston, 1998), generating numbers which are fed into the Box-Muller transform to generate the normal distribution associated with the Wiener process. Besides providing a simulator of the Wiener process, the WIENER program can also be used in a "lock-in" mode with zero expectation value for each data point, providing a pretty good random number generator for large series of stochastic data, not relying on the (rather poor) generators available in standard C libraries.
The WIENER program does not solve any problem per se, but is merely to be considered as a generator of statistical data to be used by other applications in modeling of physical, chemical or financial processes.
For an extensive description of the algorithms used in the program, supported command-line options and syntax, as well as the full documentation of the source, see wiener.pdf. [348 kB, 27 pages].
The Wiener process
To quote Wikipedia on the Wiener process:
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown. It is one of the best known Lévy processes (càdlàg stochastic processes with stationary independent increments) and occurs frequently in pure and applied mathematics, economics and physics.
The Wiener process plays an important role both in pure and applied mathematics. In pure mathematics, the Wiener process gave rise to the study of continuous time martingales. It is a key process in terms of which more complicated stochastic processes can be described. As such, it plays a vital role in stochastic calculus, diffusion processes and even potential theory. It is the driving process of Schramm–Loewner evolution. In applied mathematics, the Wiener process is used to represent the integral of a Gaussian white noise process, and so is useful as a model of noise in electronics engineering, instrument errors in filtering theory and unknown forces in control theory.
The Wiener process has applications throughout the mathematical sciences. In physics it is used to study Brownian motion, the diffusion of minute particles suspended in fluid, and other types of diffusion via the Fokker–Planck and Langevin equations. It also forms the basis for the rigorous path integral formulation of quantum mechanics (by the Feynman–Kac formula, a solution to the Schrödinger equation can be represented in terms of the Wiener process) and the study of eternal inflation in physical cosmology. It is also prominent in the mathematical theory of finance, in particular the Black–Scholes option pricing model.
What the WIENER program does (and doesn't)
The present CWEB [1] program does not solve any problems related to any of the processes described by models involving the Wiener process, but is merely an attempt to produce an as-good-as-possible result when simulating the Wiener process as such. In the WIENER program, special attention has been paid to the generation of random numbers, as this is a crucial and rather tricky problem when it comes to generating large non-recurring series of data. In the present program, the random number generator proposed by Donald Knuth in The Art of Computer Programming, Volume 1 – Fundamental Algorithms, 3rd edition (Addison-Wesley, Boston, 1998) has been employed, generating uniformly distributed numbers which are fed into the Box–Muller transform to generate the normal distribution associated with the Wiener process.
Apart from being a pretty good and reliable generator of statistical data, to be used by other applications in modeling of physical, chemical or financial processes, the WIENER program does not solve any problems per se.
Current revision
Revision 1.0, as of 11/11/2011. Copyright © Fredrik Jonsson 2011, under GPL. Non-commercial copying welcome.
Source files
wiener.pdf [348 kB] Documentation of the Wiener program in Portable Document Format (PDF) [3], generated from the PostScript [5] documentation.
wiener.w
[53 kB]
The CWEB [1] master source code for the WIENER program.
From this master, the ANSI-C (ISO C90) source code for the program and TeX
code for the documentation is extracted using the CTANGLE and CWEAVE
compilers, respectively.
[ download |
view source ]
Makefile
[4 kB]
The Makefile for compilation of the executable file, as well as generation
of the documentation of the program. Extracts the C and TeX code from the
CWEB source, and compiles the C and TeX code into binary executable and
PostScript, respectively.
To compile the executable and documentation, simply run 'make' in the
directory containing the source files and this Makefile.
[ download |
view source ]
wiener.c
[9 kB]
ANSI-C (ISO C90) conforming source code, extracted from the CWEB master
source code using the CTANGLE program by Donald E. Knuth.
[ download |
view source ]
wiener.tex
[61 kB]
Plain TeX [4] source code, extracted from the CWEB master
source code using the CWEAVE program by Donald E. Knuth.
[ download |
view source ]
wiener.ps [1.27 MB] PostScript [5] documentation of the Wiener program, generated from the TeX-code, which in turn is generated from the CWEB master source code.
wiener.tar.gz
[590 kB]
Gzip:ed
tape archive of
the entire Wiener program directory, including the CWEB
[1] master source code source, Makefile:s and all
examples needed to rebuild the program and documentation from scratch.
Requires
CTANGLE and
CWEAVE.
[ download ]
Compilation
Compile the CWEB [1] code wiener.w using the enclosed Makefile, or use the blocks of the Makefile as listed in the documentation.
The Wiener program is written in CWEB [1], generating ANSI-C (ISO 9899/C90) conforming source code and documentation as plain TeX [4] source, and is to be compiled using the sequences as outlined in the enclosed Makefile. The Makefile essentially executes two major calls. First, the CTANGLE program parses the CWEB source document wiener.w to extract a ANSI-C source file wiener.c, which may be compiled in the usual way using any ANSI-C conformant compiler. The output source file includes #line specifications so that any debugging can be done conveniently in terms of the original CWEB source file. Second, the CWEAVE program parses the same CWEB source file to extract a plain TeX source file wiener.tex which may be compiled in the usual way. It takes appropriate care of typographic details like page layout and the use of indentation, italics, boldface, and so on, and it supplies extensive automatically gathered cross-index information.
After having executed make in the same catalogue where the files wiener.w and Makefile are located, one is left with an executable file wiener, being the ready-to-use compiled program, and a PostScript file wiener.ps [5] which contains the full documentation of the program. Notice that on platforms running Windows NT, Windows 2000, Windows ME, or any other operating system by Microsoft, the executable file will instead automatically be called wiener.exe. This convention also applies to programs compiled under the UNIX-like environment CYGWIN.
Precompiled executables
wiener [18 kB] Executable program compiled for Mac OS X 10.7 (Lion) using the GNU C Compiler (GCC). [Compiled Friday 16 Dec, 2011]
Running the program
The Wiener program is entirely controlled by the command line options supplied when invoking the program. The syntax for executing the program is
wiener [options]
where options include the following, given in their long (--) as well as their short (-) forms:
--help, -h
Display a brief help message and exit clean.
--verbose, -v
Toggle verbose mode. Default: off.
--num_samples M, -M M
Generate M samples of data. Here M should always be an even number, greater than the long lag KK (see enclosed documentation for details). If an odd number is specified, the program will automatically adjust this to the next higher (even) integer. Default: M = KK = 100.
--dimension D, -D D
Specifies the dimension D of the Wiener process, that is to say generating a set of D numbers for each of the M data points in the seqence. Default: D = 1.
--seed S, -S S
Define a custom seed number S for the initialization of the random number generator (see enclosed documentation for details). Default: S = DEFAULT_SEED = 310952.
--uniform, -u
Instead of generating a sequence of data corresponding to a Wiener process, lock the program to simply generate a uniform distribution of D-dimensional points, with each element distributed over the interval [0,1].
--normal, -n
Instead of generating a sequence of data corresponding to a Wiener process, lock the program to simply generate a normal distribution of D-dimensional points, with each element distributed with zero expectation value and unit variance.
One may look upon the two last options as verification options, generating data suitable for spectral tests on the quality of the generator of pseudo-random numbers.
Displaying the results using GNUPLOT or MetaPost
The data sets generated by WIENER may be displayed and saved as Encapsulated PostScript images [5] using, say, GNUPLOT or MetaPost. While I personally prefer MetaPost, mainly due to the possibility of incorporating the same typygraphic elements as in TeX, many people consider GNUPLOT to be easier in operation.
In order to save a scatter graph as Encapsulated PostScript using GNUPLOT, you may include the following calls in, say, a Makefile or a shell script:
wiener -D 2 -M 10000 > figure.dat;
echo 'set term postscript eps;\
set output "figure.eps";\
set size square;\
set nolabel;\
plot "figure.dat" with dots notitle;\
quit' | gnuplot
Another choice is to go for the MetaPost way. This is illustrated with the following blocks, taken directly from the enclosed Makefile and generating the figures which can be seen in the section relating to the generation of normally distributed variables (routine normdist):
PROJECT = wiener
TEX = tex
DVIPS = dvips
METAPOST = mpost
#
# Generate the Encapsulated PostScript image fig1.eps for the
# documentation. This is a 2D scatter plot of the uniformly
# distributed pseudo-random numbers prior to having been fed
# into the Box-Muller transform.
#
fig1.eps: Makefile $(PROJECT).w
wiener --uniform -D 2 -M 10000 > fig1.dat;
@echo 'input graph;\
def mpdot = btex\
{\\vrule height 0.5pt width 1.0pt depth 0.5pt}\
etex enddef;\
beginfig(1);\
draw begingraph(86mm,86mm);\
setrange(0,0,1,1);\
pickup pencircle scaled .5pt;\
gdraw "fig1.dat" plot mpdot;\
pickup pencircle scaled .25pt;\
autogrid(itick bot,itick lft);\
glabel.bot(btex $$ x$$ etex,OUT);\
glabel.lft(btex $$ y$$ etex,OUT);\
endgraph; endfig; end' > fig1.mp
$(METAPOST) fig1.mp
$(TEX) -jobname=fig1 "\input epsf\nopagenumbers\
\centerline{\epsfbox{fig1.1}}\bye"
$(DVIPS) -D1200 -E fig1.dvi -o fig1.eps
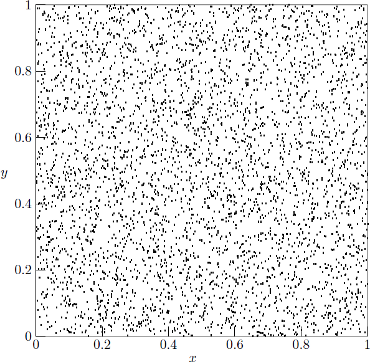
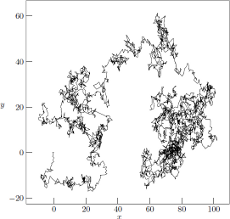
Figure 1. Sample two-dimensional output from the ranf_matrix() routine, in this case 10 000 data points uniformly distributed over the domain 0≤{x, y}≤1. The data for this graph was generated by the WIENER program using wiener --uniform -D 2 -M 10000 > fig1.dat. See the fig1.eps block in the enclosed Makefile for details on how MetaPost was used in the generation of the encapsulated PostScript image of the graph.
Encapsulated PostScript [5] image fig1.eps [311 kB].
#
# Generate the Encapsulated PostScript image fig2.eps for the
# documentation. This is a 2D scatter plot of the normally
# distributed pseudo-random numbers resulting from the Box-Muller
# transform.
#
fig2.eps: Makefile $(PROJECT).w
wiener --normal -D 2 -M 10000 > fig2.dat;
@echo 'input graph;\
def mpdot = btex\
{\\vrule height 0.5pt width 1.0pt depth 0.5pt}\
etex enddef;\
beginfig(1);\
draw begingraph(86mm,86mm);\
setrange(whatever,whatever,whatever,whatever);\
pickup pencircle scaled .5pt;\
gdraw "fig2.dat" plot mpdot;\
pickup pencircle scaled .25pt;\
autogrid(itick bot,itick lft);\
glabel.bot(btex $$ x$$ etex,OUT);\
glabel.lft(btex $$ y$$ etex,OUT);\
endgraph; endfig; end' > fig2.mp
$(METAPOST) fig2.mp
$(TEX) -jobname=fig2 "\input epsf\nopagenumbers\
\centerline{\epsfbox{fig2.1}}\bye"
$(DVIPS) -D1200 -E fig2.dvi -o fig2.eps
Figure 2. The same data points as in Fig. 1, but after having applied the Box–Muller transform to yield a normal distribution of pseudo-random numbers. The data for this graph was generated by WIENER using wiener --normal -D 2 -M 10000 > fig2.dat. See the fig2.eps block in the enclosed Makefile for details on how MetaPost was used in the generation of the encapsulated PostScript image of the graph.
Encapsulated PostScript [5] image fig2.eps [323 kB].
#
# Generate the Encapsulated PostScript image fig3.eps for the
# documentation. This is a 2D graph showing the resulting
# simulated Wiener process.
#
fig3.eps: Makefile $(PROJECT).w
wiener -D 2 -M 10000 > fig3.dat;
@echo 'input graph;\
beginfig(1);\
draw begingraph(86mm,86mm);\
setrange(whatever,whatever,whatever,whatever);\
pickup pencircle scaled .5pt;\
gdraw "fig3.dat";\
pickup pencircle scaled .25pt;\
autogrid(itick bot,itick lft);\
glabel.bot(btex $$ x$$ etex,OUT);\
glabel.lft(btex $$ y$$ etex,OUT);\
endgraph; endfig; end' > fig3.mp
$(METAPOST) fig3.mp
$(TEX) -jobname=fig3 "\input epsf\nopagenumbers\
\centerline{\epsfbox{fig3.1}}\bye"
$(DVIPS) -D1200 -E fig3.dvi -o fig3.eps
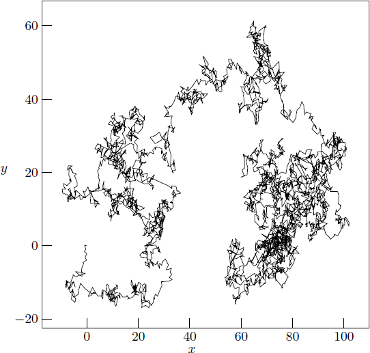
Figure 3. The same data points as in Fig. 2, but after having chained the normally distributed points to form the simulated Wiener process. The data for this graph was generated by WIENER using wiener -D 2 -M 10000 > fig3.dat. The trajectory starts with data point 1 at (0,0) and end up with data point 10 000 at approximately (89.9,12.6). See the fig3.eps block in the enclosed Makefile for details on how MetaPost was used in the generation of the encapsulated PostScript image of the graph.
Encapsulated PostScript [5] image fig3.eps [160 kB].
References
[1] For information on the CWEB programming language as written by Donald E. Knuth, as well as samples of CWEB programs, see Knuth's homepage at http://www-cs-faculty.stanford.edu/~knuth/cweb.html For information on literate programming, as well as additional CWEB examples, see http://www.literateprogramming.com
[2] MetaPost is both a programming language and the only known interpreter of the MetaPost programming language. Both are derived from Donald E. Knuth's Metafont language and interpreter. The language shares Metafont's elegant declarative syntax for manipulating lines, curves, points and geometric transformations [Wikipedia]. The originator of MetaPost, John Hobby, has a page on the MetaPost language at http://cm.bell-labs.com/who/hobby/MetaPost.html. The TeX Users Group (TUG) has tutorials and links to MetaPost resources listed at http://www.tug.org/metapost.html.
[3] For information on the Portable Document Format (PDF) of Adobe, see for example the homepage of Adobe Systems Inc., at http://www.adobe.com/products/acrobat/
[4] For information on the TeX typesetting system, as well as on the dvips program, see for example the website of the TeX Users Group, at http://www.tug.org
[5] For information on the PostScript programming language, see for example the PostScript area on the website of Adobe Systems Inc., at http://www.adobe.com/products/postscript/ or the reference book "PostScript Language - Tutorial and Cookbook" (Adison-Wesley, Reading, Massachusetts, 1985), ISBN 0-201-10179-3.