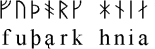Computer programs
»Where shall I begin, please your Majesty?» he asked »Begin at the beginning,» the King said, gravely, »and go on till you come to the end: then stop.»
– Lewis Carroll, Alice's Adventures in Wonderland.
For quite some time now, I have been thinking about publicly releasing the source code for a set of the programs I have written over the years, so here we go. Please help yourself to whatever you find useful at this site.
Most of the programs you will find at this site are written in CWEB, which is a dialect of literate programming, or ANSI/ISO-conformant plain C, for the simple reason that I am a fan of standards. In particular, by using highly standardized and non-proprietary languages such as plain C or even Fortran, I find that my daily work becomes easier as I can benefit from things that have been developed earlier, either by myself or by someone else.
All code that you will find at this site has been verified to pass compilation using GCC (C/CWEB) or G77 (Fortran) with supplied -Wall -pedantic (strict) options. This implies that the code should pass compilation successfully using virtually any C or Fortran compiler. However, should you find that any code you downloaded from jonsson.eu does not pass strict compilation mode of your specific compiler, please let me know as I will be genuinely curious to know what failed.
Selected code
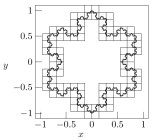
Estimating the fractal (Hausdorff) dimension of curves in the plane
The BoxCount computer program calculates box-counting estimates of the fractal dimension of curves in the two-dimensional plane. In the box-counting estimate to the fractal dimension of a curve in the domain {x, y : xmin ≤ x ≤ xmax, ymin ≤ y ≤ ymax}, a grid of squares, each of horizontal dimension (xmax - xmin) / 2m and vertical dimension (ymax - ymin) / 2m, is superimposed onto the graph for integer numbers m. By counting the total number of such squares Nm needed to cover the entire graph at a given m (hence the term »box counting»), an estimate Dm to the fractal dimension D (or Hausdorff dimension) is obtained as Dm = ln(Nm)/ln(2m). This procedure may be repeated many times, with Dm → D as m→∞ for real fractal sets. However, for finite-depth fractals (as generated by a computer), some limit on m is necessary in order to prevent trivial convergence towards Dm → 1. In addition to mere numerical calculation, the BoxCount program also generates graphs of the box distributions, in form of MetaPost code which can be post-processed by other programs.
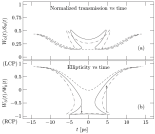
Simulating the electrodynamics of nonlinear magneto-optical Bragg gratings
The MagBragg computer program calculates reflection and transmission spectra of nonlinear magneto-optical Bragg gratings, in a stratified geometry where the material parameters vary only in one Cartesian coordinate. The MagBragg program also simulates the propagation of the electromagnetic field of an optical wave as it traverses a magneto-optical Bragg grating, giving the intra-grating spatial distribution of the optical fields in linear as well as nonlinear optical regimes. The MagBragg program forms the core behind the semi-analytical algorithm that in 2006 was published in Phys. Rev. Lett. 96, 063902 (2006). The MagBragg program is written in CWEB.
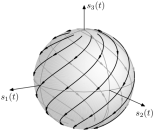
Topological mapping of trajectories of Stokes parameters on the Poincaré sphere
The Poincare computer program creates topographic maps of Stokes parameters, visualized as trajectories on the Poincare sphere. The Poincare program generates MetaPost source code as output, to be compiled into PostScript or Encapsulated PostScript, using John Hobby's MetaPost compiler or anything that understands the MetaPost syntax. I originally wrote the Poincare program back in 1997, after which it has been continuously updated and modified. In fact, this is program I keep active in my stock. This program was used in the generation of the image that made it to the front page of issue 4 of J. Opt. A: Pure Appl. Opt., Vol. 2 (July 2000).
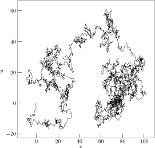
Simulating the Wiener process in D dimensions.
The WIENER program computes a series of floating-point numbers corresponding to a Wiener process in D dimensions. The program relies on the random number generator as proposed by Donald Knuth in The Art of Computer Programming, Volume 1 – Fundamental Algorithms, (Addison-Wesley, Boston, 1998), generating numbers which are fed into the Box–Muller transform to generate the normal distribution associated with the Wiener process. Besides providing a simulator of the Wiener process, the WIENER program can also be used in a "lock-in" mode with zero expectation value for each data point, providing a pretty good random number generator for large series of stochastic data, not relying on the (rather poor) generators available in standard C libraries. The WIENER program does not solve any problem per se, but is merely to be considered as a generator of statistical data to be used by other applications in modeling of physical, chemical or financial processes.
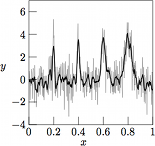
The Savitzky-Golay smoothing filter
The SGFilter computer program provides a stand-alone implementation of the Savitzky-Golay smoothing filter. This filter was originally proposed in 1964 by Abraham Savitzky and Marcel Golay as an algorithm of recovering feature characteristics from noisy spectra, overcoming the drawbacks of simpler noise-reduction techniques such as running averages. The work-around presented by Savitzky and Golay for avoiding distortion of peaks or features in their spectral data is essentially based on the idea to perform a linear regression of some polynomial individually for each sample, followed by the evaluation of that polynomial exactly at the very position of the sample. While this may seem a plausible idea, the actual task of performing a separate regression for each point easily becomes a very time-consuming task. However (and this is the key point in the Savitzky-Golay algorithm), the coefficients involved in the actual regression may be computed once and for all in an early stage, followed by performing a convolution of the discretely sampled input data with the coefficient vector.
Multiline LCD display driver for the Microchip PIC32 family of microcontrollers
This driver provides support for terminal output to the Electronic Assembly DOG-M family of LCD displays, interfacing microcontrollers of the Microchip PIC32 family. The driver supports full ASCII functionality such as carriage return, backspace commands, line wrapping and arbitrary positioning of character output within the display, employing the Parallel Master Port (PMP) of the PIC32.
Creating a PIC32 project from scratch using the Microchip MPLAB IDE
This document summarizes the steps when creating a new project for the Microchip PIC32 family of microcontrollers, using the MPLAB® IDE. The document summarizes all settings and configurations needed to get a stable project release up and running. The specific example illustrated in this checklist is the driver for the DOGM-163 LCD display, included in the shared library libdogm16x.a.
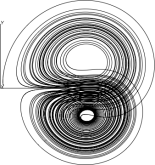
Solving systems of ordinary differential equations directly in the PostScript programming language
The odesolv.ps program illustrates the solving of systems of ordinary differential equations (ODEs) directly in the PostScript programming language, here specifically illustrated for the 3D trajectory of the Lorenz attractor. The instructions defined in the supplied routines are typically interpreted by either a PostScript viewer (such as GhostView with GhostScript as the interpreting engine) or the PostScript interpretor of your printer (in which case no computation is performed by your local computer, putting the whole task into the hands of your printer).
Creating Encapsulated PostScript (EPS) images of arrayed data
Given a matrix of floating-point numbers stored in a regular ASCII text file, the EpsImg program creates a grey-scale Encapsulated PostScript (EPS) image of the matrix using its elements as specification of the brightness of the corresponding pixels in the image. Of course, there are other ways of generating Encapsulated PostScript images of sampled of simulated data, as for example using the image() function of MATLAB. However, an advantage with using a stand-alone program is that it is easily incorporated in scripts for batch processing. In addition, the EpsImg program is provided free of charge. The EpsImg program is written in the CWEB programming language; however, as it is targeted towards generation of Encapsulated PostScript, the main entry for this program is under the PostScript programs section.
Generating TeX source code for the typesetting of labels for digital video tapes
The DvLabel computer program generates plain TeX source code for typesetting of labels for digital video tapes (DV format, typically used for hand-held video camera recorders). The DvLabel program is primarily designed to run in interactive mode, but via command-line supplied parameters it also supports batch-mode operation. I got the idea of creating this program from the audio-tape.ps PostScript code by Jamie Zawinski. The audio-tape.ps code is a splendid example of how one can write a simple PostScript program with the help of a regular ASCII editor, and by sending the PostScript program to the printer one gets a neat printout to be used for tape cassette labels, DAT, or video tapes. However, whenever one has a new cassette to be labeled, one has to edit the PostScript source, and for a rookie on PostScript programming this task is for sure somewhat inconvenient. (Believe me.) The DvLabel program is written in CWEB.
Unclassifiable programs
The Futhark (Runic alphabet) on a HP-42S calculator
The FUTH program is written for the HP-42s calculator and displays strings of characters from the futhark (used in historic Scandinavia, also denoted Runic alphabet) as supplied by the user via a two-level menu system. The input characters are in the user interface of the program listed as we would read and pronounce them today. (Written sometime in early 1990.)